How Pendulum Clocks Work

As we stated on the previous page, the only thing affecting the period of a pendulum is the length of that pendulum. You can prove this fact to yourself by performing the following experiment. For this experiment you will need:

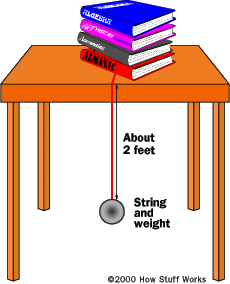
For the weight you can use anything. In a pinch, a coffee mug or a book will do -- it doesn't really matter. Tie the string to the weight. Then suspend your pendulum over the edge of the table so that the length of the pendulum is about 2 feet.

Now pull the weight back about a foot and let your pendulum start swinging. Time it for 30 or 60 seconds and count how many times it swings back and forth. Remember that number. Now stop the pendulum and restart it, but this time pull it back only 6 inches initially so it is swinging through a much smaller arc. Count the number of swings again through the same 30- or 60-second time period. What you will find is that the number you get is the same as the first number you counted. In other words, the angle of the arc through which the pendulum swings does not affect the pendulum's period. Only the length of the pendulum's string matters. If you play around with the length of your pendulum you will find that you can adjust it so that it swings back and forth exactly 60 times in one minute.

(Note: If you want to be exactly accurate about the pendulum period, see this interesting article.)

Once someone noticed this fact about pendulums, it was realized that you could use the phenomenon to create an accurate clock. The figure below shows how you can create a clock's escapement using a pendulum.

In an escapement there is a gear with teeth of some special shape. There is also a pendulum, and attached to the pendulum is some sort of device to engage the teeth of the gear. The basic idea that is being demonstrated in the figure is that, for each swing of the pendulum back and forth, one tooth of the gear is allowed to "escape."

For example, if the pendulum is swinging toward the left and passes through the center position as shown in the figure on the right, then as the pendulum continues toward the left the left-hand stop attached to the pendulum will release its tooth. The gear will then advance one-half tooth's-width forward and hit the right-hand stop. In advancing forward and running into the stop, the gear will make a sound... "tick" or "tock" being the most common. That is where the ticking sound of a clock or watch comes from!

One thing to keep in mind is that pendulums will not swing forever. Therefore, one additional job of the escapement gear is to impart just enough energy into the pendulum to overcome friction and allow it to keep swinging. To accomplish this task, the anchor (the name given to the gizmo attached to the pendulum to release the escapement gear one tooth at a time) and the teeth on the escapement gear are specially shaped. The gear's teeth escape properly, and the pendulum is given a nudge in the right direction by the anchor each time through a swing. The nudge is the boost of energy that the pendulum needs to overcome friction, so it keeps swinging.

So, let's say that you create an escapement. If you gave the escapement gear 60 teeth and attached this gear directly to the weight drum we discussed above, and if you then used a pendulum with a period of one second, you would have successfully created a clock in which the second hand turns at the rate of one revolution per minute. By adjusting the pendulum's length very carefully we could create a clock with very high accuracy.

However, while accurate, this clock would have two problems that would make it less-than-useful:

So, what does it take to solve the winding problem? Read on...