AI chess is fairly intricate, but it involves blind computation that is very simple at the core.
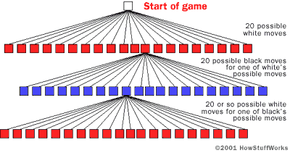
Let's say you start with a chessboard set up for the start of a game. Each player has 16 pieces. Let's say that white starts. White has 20 possible opening moves:
- The white player can move any pawn forward one or two chess positions.
- The white player can move either knight in two different ways.
The white player chooses one of those 20 moves and makes it.
For the black player, the options are the same: 20 possible moves. So black chooses a move.
Now white can move again. This next move depends on the first move that white chose to make, but there are about 20 or so moves white can make given the current board position, and then black has 20 or so moves it can make, and so on.
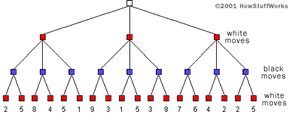
This is how a computer looks at chess. It thinks about it in a world of "all possible moves," and it makes a big tree for all of those moves, like this:
In this tree, there are 20 possible moves for white. There are 20 * 20 = 400 possible moves for black, depending on what white does. Then there are 400 * 20 = 8,000 for white. Then there are 8,000 * 20 = 160,000 for black, and so on. If you were to fully develop the entire tree for all possible chess moves, the total number of board positions is about
1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 or 10120 — give or take a few.
That's a very big number. For example, there have only been 1026 nanoseconds since the Big Bang. There are thought to be only 1075 atoms in the entire universe. When you consider that the Milky Way galaxy contains billions of suns, and there are billions of galaxies, you can see that that's a whole lot of atoms. But that number is dwarfed by the number of possible chess moves. Chess is a pretty intricate game!
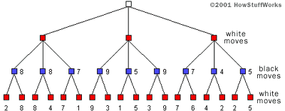
No computer is ever going to calculate the entire tree. What a chess computer tries to do is generate the board-position tree five or 10 or 20 moves into the future. Assuming there are about 20 possible moves for any board position, a five-level tree contains 3,200,000 board positions. A 10-level tree contains about 10,000,000,000,000 (10 trillion) positions. The depth of the tree that a computer can calculate is controlled by the speed of the computer playing the game. The fastest chess computers can generate and evaluate millions of board positions per second.
Once it generates the tree, the computer needs to "evaluate the board positions." Using a search algorithm, the AI explores possible moves and outcomes several levels ahead in the game. However, to decide which move is optimal, it must assign a value to each board position it encounters. This is where the evaluation function comes into play. For example, if the computer is playing white and a certain board position has 11 white pieces and nine black pieces, the simplest evaluation function might be:
Obviously, that formula is way too simple for chess — after all, some chess pieces are more valuable than others. So the formula might apply a weight to each type of piece. As the programmer thinks about it, they make the evaluation function more and more complicated by adding things like board position, control of the center, vulnerability of the king to check, vulnerability of the opponent's queen, and tons of other parameters. No matter how complicated the function gets, however, it's condensed down to a single number that represents the "goodness" of that board position.